Utilisation des nombres nombres complexes en électricité

Rappel sur les nombres complexes ( application au domaine de l’électricité) :
La notation complexe remplace avantageusement la représentation de Fresnel puisqu’elle permet d’éviter la représentation graphique des vecteurs. Dans l’ensemble des nombres réels, un vecteur plan est représenté par deux coordonnées x et y.
En complexe ce même vecteur pourra être représenté par une équation mathématique.
le symbole habituellement utilisé en mathématique pour représenter un imaginaire pur et la lettre i .
En physique, cette lettre est déjà couramment utilisée pour représenter un courant, d’où le choix de la lettre j .
j: est un nombre complexe d’argument égale à π/2 et de module égal à 1 tel que j² = -1.
Représentation des nombres complexes
Soit un nombre complexe :
z =a +j b : sous la forme algébrique
On peut le représenter avec des coordonnées polaires
si un nombre complexe : z=a +jb= Z e jj
Alors le complexe conjugué de z est z*= a-jb = Z e-jj
Ce qui revient à : ej0 = 1 ; ejπ/2= j , et e-jπ/2= -j et ejπ = -1
Opération sur des nombres complexes
Addition, soustraction de nombres complexes
On utilise de préfèrence la notation cartésienne ( dites aussi algébrique) .
Soit deux nombres complexes : z1= a+jb et z2=c+jd alors z1+z2= (a+c)+j(b+d)
Inverse d’un nombre complexe
Dans ce cas on utilise de préférence la notation polaire: soit le complexe y=Y e jβ tel que y=1/z
Alors : y=Y e jβ= 1⁄z = 1 /( Zejj ) = 1/( Z).e-jj On en déduit que : Y = 1 / Z et β=-φ
Si z =[Z;φ] alors y=1/z= [1/Z;-φ]
Produit et division de deux nombres complexes
On utilise de préférence la notation polaire.
Soient deux complèxes:z1=Z1 e(jφ1) et z2=Z2 e(jφ2) alors le produit : z1. z2=Z1.Z2ej(φ1+φ2)
et le rapport z1/z2 = Z1/Z2.ej (φ1– φ2)
Représentation complexe des grandeurs électriques
Tension et courant
Comme pour la représentation de Fresnel, le module est la valeur efficace U et l’argument la phase à l’origine θu .
équation horaire |
écriture exponentielle |
écriture polaire |
|---|---|---|
u(t)= U√2 sin(ωt+θu) |
U=U.ejθu |
U =[U,θu] |
i(t)= I√2sin(ωt+θi) |
I=I.ejθi |
I =[I,θi] |
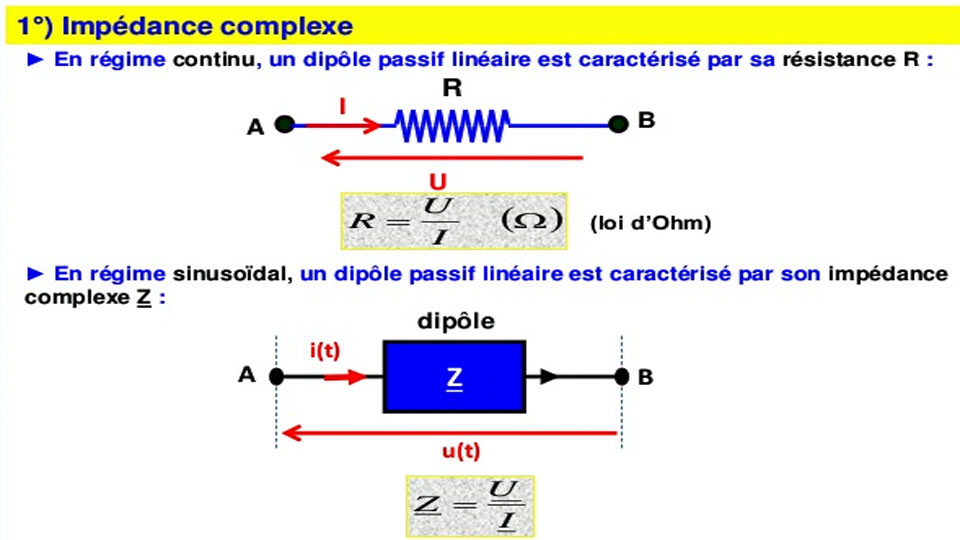
Impédance et admittance d’un dipôle
Si on considère un dipôle d’impédance z .
On exprime une impédance complexe par la relation : z= Z ejj
Z est le module de l’impédance en ohms (W)
j : est le déphasage introduit par le dipôle entre la tension u aux bornes du dipôle et le courant i qui le traverse ( j en radians – rad).
Ce qui donne pour les dipôles élémentaires R, L et C
Tableau des impédances complexes élémentaires
Dipôle\Impdénace |
Forme exponentielle |
forme polaire |
|---|---|---|
Résistance ( R) |
zR= R |
zR=[R;0] |
Inductance(L) |
zL= jLω |
zL=[Lω;π/2] |
Condensateur (C) |
zC= -j/(C .ω) |
zC=[1/(C.ω);-π/2] |
L’admittance y d’un dipôle est l’inverse de l’impédance z de ce même dipôle.
Tableau des admittances complexes élémentaires
Dipôle\admittance |
Forme exponentielle |
forme polaire |
|---|---|---|
Résistance ( R) |
yR= 1/R |
yR=[1/R;0] |
Inductance(L) |
yL= -j/Lω |
yL=[1/Lω;-π/2] |
Condensateur (C) |
yC= j.C .ω |
zC=[C.ω;+π/2] |
Associations de dipôles
Principe
On généralise aux impédances complexes ce que l’on connaît déjà pour la résistance.
Si les dipôles sont en séries, l’impédance équivalente est la somme des impédances.
z = z1+z2+z3
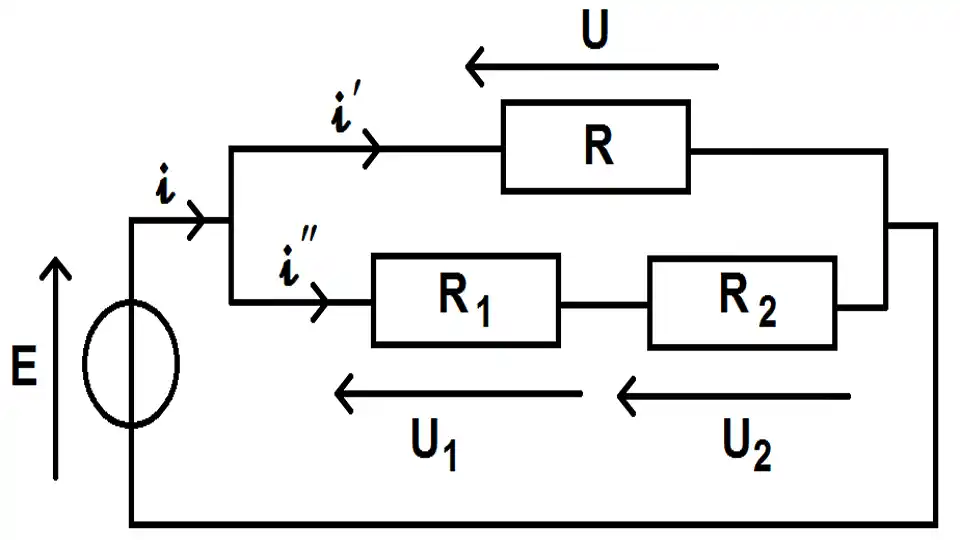
Si les dipôles sont en parallèles, l’admittance équivalente est la somme des admittances.
y= y1+y2+y3
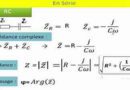
La résonance:
Il y a une fréquence particulière f0 dite fréquence de résonance, c’est la fréquence qui vérifie l’équation Im(z) = 0 (partie imaginaire de l’impédance z nulle).
Pour un circuit (R,L,C) série cette fréquence f0 est telle que L.C.ω02= 1 ( avec ω0= 2π.f0).
Pour cette fréquence on risque d’avoir des surtensions aux bornes de l’inductance L et du condensateur C, en effet à la résonance l’intensité du courant dans le circuit n’est limitée que par la résistance car z= R.